問題
解説
グラフの描き方グラフを描く基本は、点をたくさんとって結ぶ、ということです。
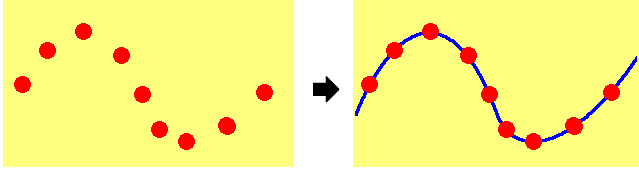
一次関数のグラフ
グラフの形がわかっていれば、そのぶん、少ない点でグラフを描くことができます。
たとえば、y = 2x+3 のような一次関数のときは、グラフの形が直線になるので、2つの点だけでグラフが描けます。
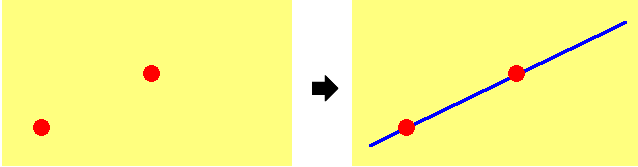
1つめの点の探し方
ふつう、1つめの点としては切片を見ます。切片が整数なら、そこが1つめの点です。
切片とは、「y = ax + b」の b のことです。これは、グラフの y 軸上の点 です。つまり、x = 0 のときの y の値です。たとえば、y = 2x - 3 のグラフの切片は -3 です。
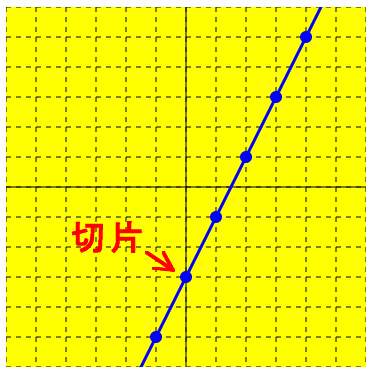
切片が分数のときは、切片をあきらめて、x も y も整数になるような点をガッツで見つけます。
このときよく、探しやすいように、式を y = ax+bc の形に変形したりします。 たとえば、y = 12x+43 のときは、12 と 43 を通分して y = 3x+86 に変形します。そして、3x+8 が 6 の倍数になるような整数 x を探すわけです。
2つめの点の探し方
2つめの点は、ガッツで探してもいいのですが、変化の割合がわかっていると見つけるのがラクです。1つめの点から、変化の割合のぶん進んだところが、2つめの点になります。
変化の割合とは、「x が 1 増えたとき、y がいくら増えるか」ということです。
たとえば、y = 2x+3 の変化の割合は 2 なので、「x が 1 増えたとき、y が 2 増える」ことがわかります。
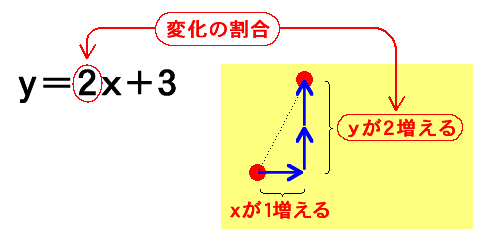
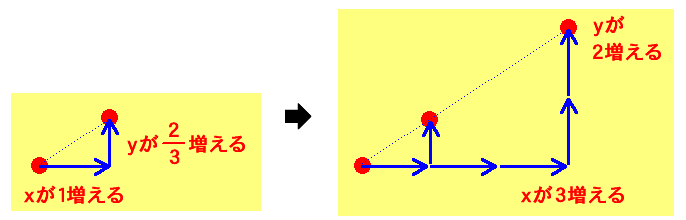
また、変化の割合が 23 のような分数のときは、「x が 1 増えたとき、y が 23 増える」をそれぞれ 3 倍して、「x が 3 増えたとき、y が 2 増える」と考えるとわかりやすいです。つまり、変化の割合が分数のときは、y の増える量x の増える量 と考えるわけです。
「変化の割合」と聞くと、なんだか難しそうですが、日常の身近なところにごくふつうにあります。
たとえば、「毎月 2000円 貯金するぞ!」というときは、1か月で貯金が2000円増えるので、1か月ごとの変化の割合は「2000円」です。
「速さが時速60km」というときは、1時間で進む距離が60km増えるので、1時間ごとの変化の割合は「60km」です。
たとえば、y = 2x+3 の変化の割合は 2 なので、「x が 1 増えたとき、y が 2 増える」ことがわかります。

また、変化の割合が 23 のような分数のときは、「x が 1 増えたとき、y が 23 増える」をそれぞれ 3 倍して、「x が 3 増えたとき、y が 2 増える」と考えるとわかりやすいです。つまり、変化の割合が分数のときは、y の増える量x の増える量 と考えるわけです。

「変化の割合」と聞くと、なんだか難しそうですが、日常の身近なところにごくふつうにあります。
たとえば、「毎月 2000円 貯金するぞ!」というときは、1か月で貯金が2000円増えるので、1か月ごとの変化の割合は「2000円」です。
「速さが時速60km」というときは、1時間で進む距離が60km増えるので、1時間ごとの変化の割合は「60km」です。
y = a のグラフ
「y = a」のグラフは、横方向の直線になります。
式の中に x が入っていないということは、x とは無関係ということです。なので、x がどんな値のときでも、y の値はいつも a になります。
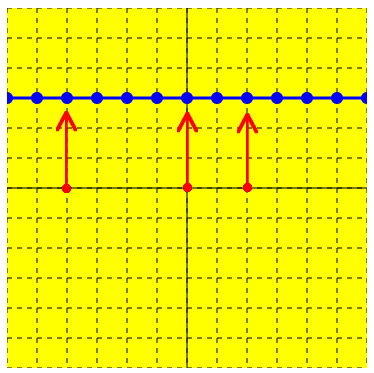
たとえば、y = 3 のグラフは、x がどんな値のときでも y の値は 3 なので、下のような横の直線になります。
x = a のグラフ
「x = a」のグラフは、縦方向の直線になります。
式の中に y が入っていないということは、y とは無関係ということです。なので、y がどんな値のときでも、x の値はいつも a になります。
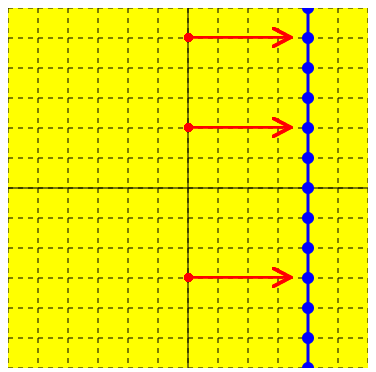
たとえば、x = 4 のグラフは、y がどんな値のときでも x の値は 4 なので、下のような縦の直線になります。



コメント